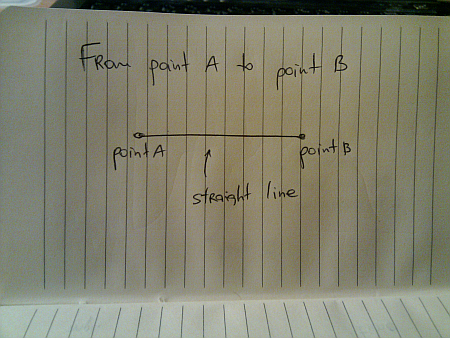
The examples in the previous entry talked about moving from point A to point B in a straight line:

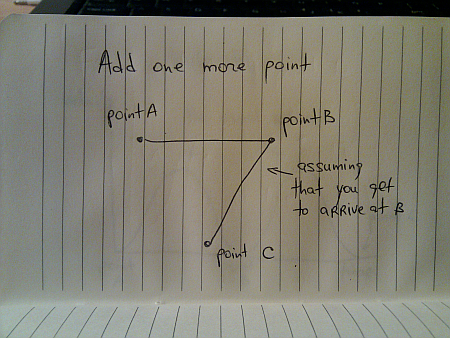
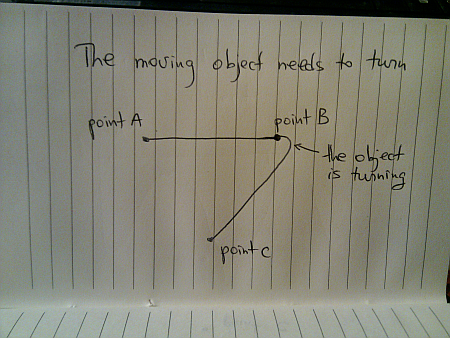
Now let’s add one more point – after arriving at point B you are asked to head to point C:

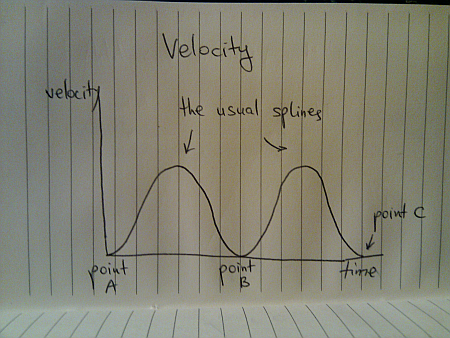
Assuming the prevalent usage of splines to approximate the acceleration and deceleration of the two segments, we have this velocity graph:

However, physical objects are not infinitely small points, and the vast majority are not perfectly symmetrical around the Z axis. To put it in a simpler term, a moving physical object has the “front” or “face” side:

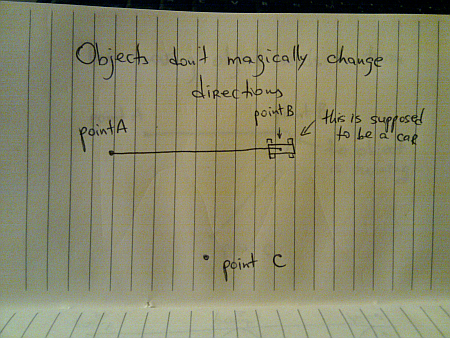
So, when the object starts moving towards C (especially if it is a man made vehicle on regular wheels), it needs to make a turn before it points to C – and can continue moving toward it in a straight line:

Even if you didn’t particularly like physics in high school, you have to deal with centrifugal force on every highway entry and exit – you have to slow down when you take the turn, otherwise your insurance policy is going to be quite expensive. On the related note – this is why outer edge of highway exits (as well as curving railroad tracks) is slightly raised.

How does the velocity graph look around point B?

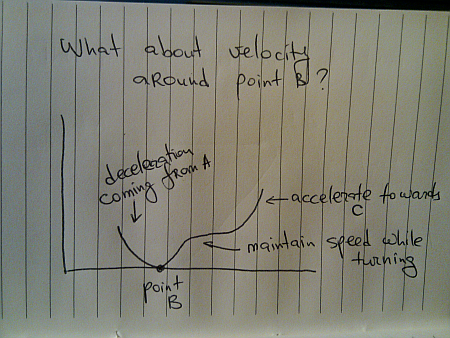
As you start turning, you accelerate until you reach speed which you deem safe to maintain as long as you are turning. Once the turn is done, you start accelerating towards the cruising speed, heading directly towards C.

Depending on what type of driver you are, you can decide to take a smaller curve and drive slower, or drive faster but take a bigger curve:

Here you can see how adding the second dimension to the movement path (since C does not lie on the line connecting A and B) adds infinite possibilities to the overall movement trajectory.

Let’s take this one step further – suppose that you are in between A and B, and are asked to move to C:

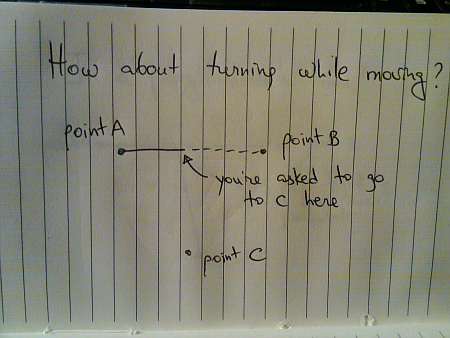
If you are on a solid plain (say, a prairie or a dry lake bed), the optimal decision is to make your turn towards C as soon as possible – without arriving at B first. Hopefully by now your solution is not going to look like this:

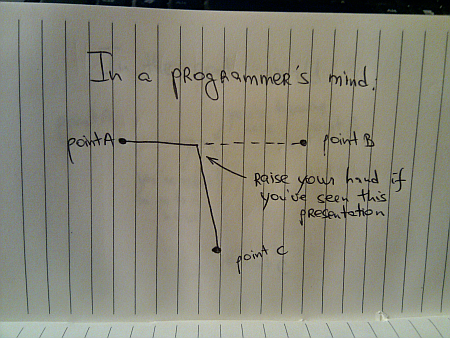
In the real world, you have two factors that will prevent this from happening. First one was mentioned above – most moving physical objects are not perfectly symmetrical around the Z axis and need to turn around to have their preferred movement direction aligned towards C. The second is due to the momentum, or inertia. If you are moving with non-zero speed towards point B, you cannot immediately switch the direction – just as you cannot immediately go from zero to your cruising speed.

Thus, the movement path is quite similar to the one seen above (when you move to C after arriving at B):

What about the velocity graph?

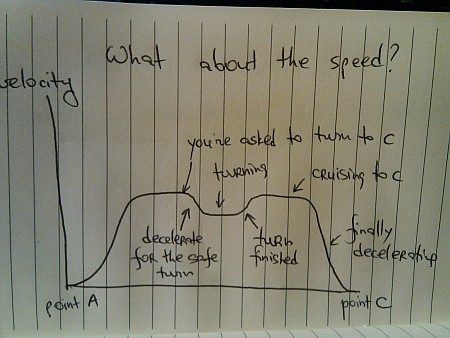
Here, you don’t need to decelerate all the way to zero speed (unless you’re a really bad driver) in order to turn your vehicle and align with C. You decelerate to your preferred turn speed, complete the turn and then accelerate back to your cruising speed (minus all the distractions along the way).

This is just one possible scenario. Here, we have been asked to turn to C while we are driving at our preferred cruising speed. What if you are asked to turn just a few moments after starting from point A – as you are still accelerating?

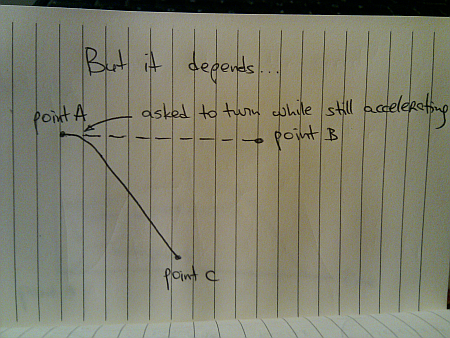
Depending on where exactly you are when this happens (specifically, whether your current speed is lower than your preferred turning speed), the velocity graph may look like this:

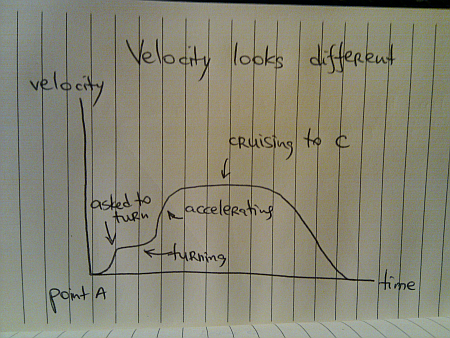
This graph assumes that you are asked to turn when you are moving at exactly your preferred turning speed. If it happens earlier, you will still be accelerating even as you begin the turn. If it happens later, you will drop your speed as you start turning, complete the turn and then accelerate towards C.

Finally, suppose you are asked to turn to C as you are decelerating and getting ready to stop at B:

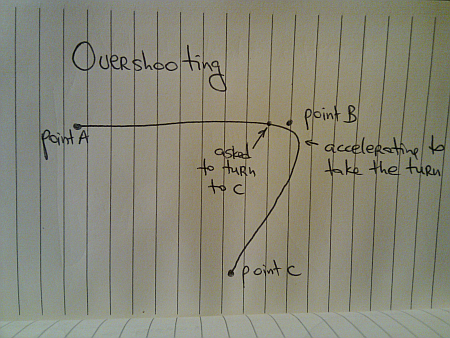
Once again, depending on your current speed you will need to either decelerate or accelerate towards your preferred turning speed, complete the turn and accelerate towards C. Depending on your preferred turning speed you may even overshoot point B as you are completing the turn.

One possible velocity graph for this scenario looks like this:

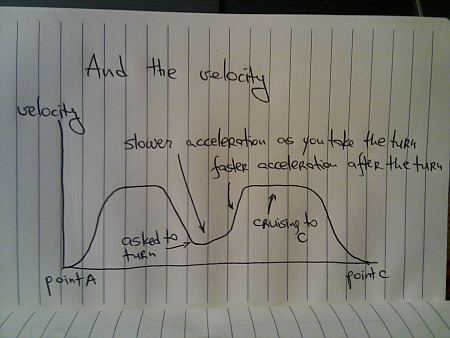
Here, the assumption is that you are asked to turn when your current speed is lower than your preferred turning speed. In this case, you start accelerating as you are turning, and then complete the acceleration after the turn is done.

As before, you see and experience all of these scenarios every day. The next time you get on or off the highway, just notice all the decisions that your body is conveying to the car – and analyze the reasons behind each one of them.

To be continued tomorrow.

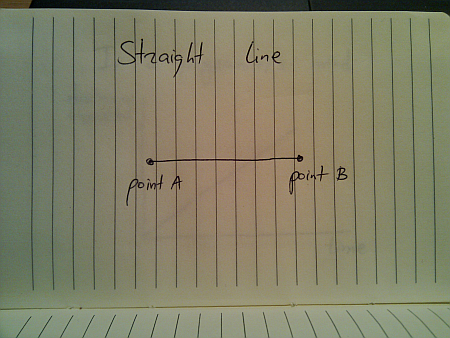
Movement is all around us in the physical world. We take it for granted since we see it from the moment we’re born. Today, i’m going to talk about a seemingly mundane act of moving from one given point to another given point. I would imagine that if you’re reading this, you most probably enjoyed your math lessons in middle school, so the following drawing should be familiar:

 

In a perfect world (imagine a deserted highway), moving from point A to point B is just following the straight line:

And if you’re a programmer, this is how you would implement this journey:

 

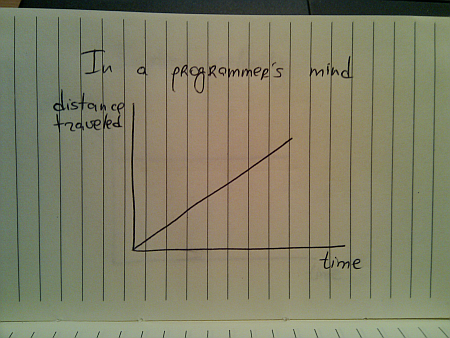
While this seems quite straightforward (and i have seen quite a few presentations that use linear animations), this falls apart once you translate the traveled distance to velocity:

 

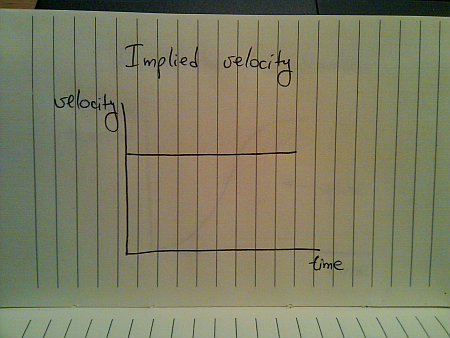
This is hardly the way things move in the real world (be they man-made, inanimate or animate). The usual approach taken by the existing animation libraries is to use a variation of spline (or perhaps a sine / cosine wave) that looks like this:

 

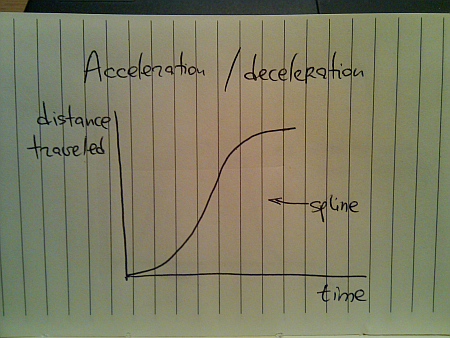
Here, you start from zero velocity, accelerate as you go, reach your maximum speed towards the middle of your journey and then start decelerating towards zero speed as you reach your destination. Translating the distance traveled to velocity, we get this:

 

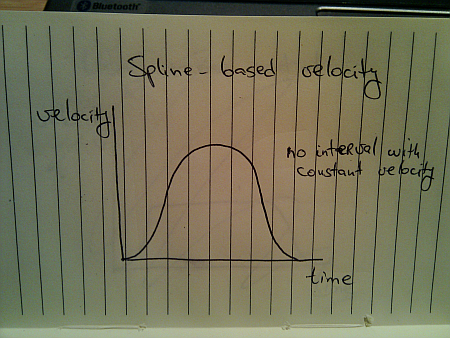
Once again, this is not how things move in the real world. A moving body (human, animal, vehicle or other) has a certain speed limit and a certain preferred speed. It takes some time to reach that speed, but once you get there, you stay until it’s time to decelerate:

 

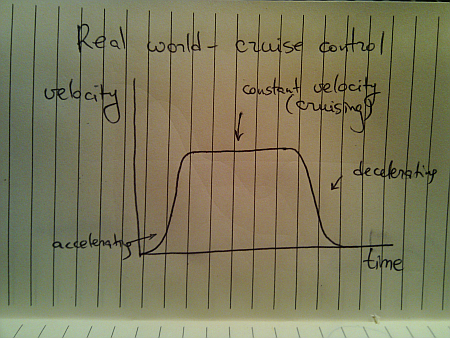
This is a better approximation of a slightly less ideal movement. The velocity graph models the “cruise control” mode that you’d employ on a deserted straight highway. Translating the velocity to distance traveled, we get this:

 

Here, we have a curving acceleration (might be a spline, a sine or even a quadratic curve – depending on the way the object is accelerating), followed by the perfectly linear segment which ends in a curving deceleration.

All the examples above assumed that you’re supposed to arrive at point B and just stop there. That is not always the case:

 

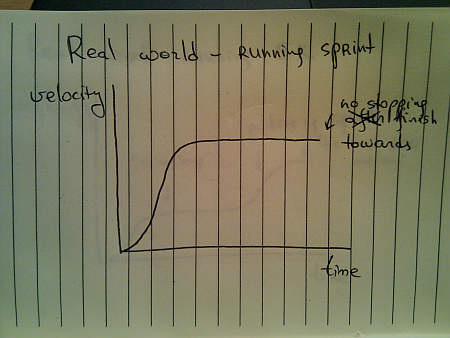
You do stop once you reach the sprint finish line, but you don’t stop until you reach it. Once you gain your maximum speed, in the ideal world you’ll be able to maintain it – especially over a very short distance.

When you’re running sprint, it doesn’t really matter what are your opponents doing. They are running on parallel tracks and do not interfere with your pace. However, if you switch from running sprint to running a longer distance (say 5K), the story gets quite different, and the most common velocity graph looks like this:

 

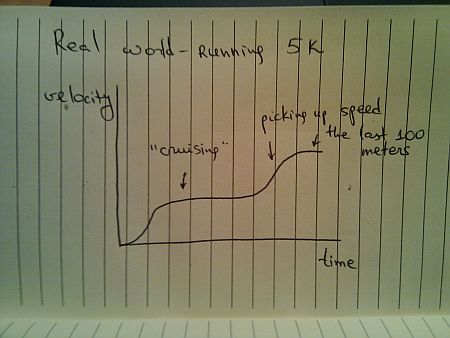
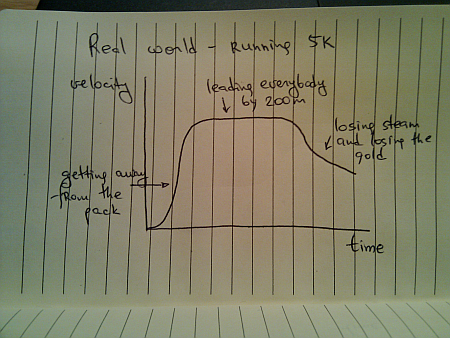
Of course, some runners try to outsmart the competition and end up running like this:

 

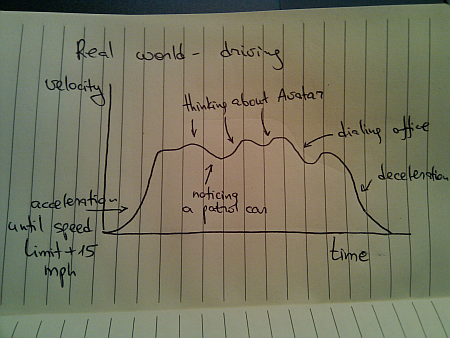
Once you leave a deserted road and have some traffic around you, you cannot always use cruise control. Even if you’re on a straight highway, your velocity graph will likely look like this:

 

Of course, these graphs are nothing new. We see countless movements of physical objects around you every day. All you need to do is look beyond the simplified approach of “train is moving with constant speed of 40mph” and start analyzing the real world.

To be continued tomorrow.

Image by Noël Zia Lee

Every month this series is tracking the latest design trends and collecting the best examples of modern web designs. Here is the list for December 2009 with over 900 links from 30 aggregator posts:

• 70 Examples of Clean & Inspiring eCommerce Sites from Designers’Couch
• 40 Beautiful and Colorful Blog Designs from hongkiat.com
• 40 Sites Showcasing Creative Use of Lighting Effects from Designers’Couch
• Minimalist Web Design: When Less is More from Webdesigner Depot
• 60+ Simply Professional Looking Website Designs from instantShift
• Bokeh Effect in Web Design: 30 Excellent Examples and Tutorials from Spyre Studios
• 50 Over the Top Retro-Vintage Website Designs from Designers’Couch
• Showcase of Creative Blogs with Totally Original Design from Inspired Magazine
• 21 Big, Bold Typography Website Design from Developer’s Paradise
• 30 Visually Appealing Corporate Website Designs from Design Reviver
• Comment Design: Considerations, Best Practices and Examples from hongkiat.com
• Design Showcase Listing 20 Websites Selling PSD To XHTML Service from Web Design Tutorials
• 55 Excellent WordPress Site Design for Design Inspiration from instantShift
• 25 Beautiful Blog Comment Designs from Vandelay Design
• 30 Website Navigations that Make You Wanna Click It from Web Design Ledger
• Breakdown of Great Web App Homepage Design from Inspect Element
• 40 Beautiful Minimalist Websites – Part 7 from Vandelay Design
• 24 Clever Website Designs That Combine jQuery and Illustration from Webdesigner Depot
• 30 Examples Of Well Designed Ecommerce Websites from Spyre Studios
• 33 “Hello” Pages Example For Your Inspiration from Developer’s Paradise
• 30 Amazing Web Design Interfaces From DeviantArt from Web Design Tutorials
• How to Get a Professional Look With Color from Webdesigner Depot
• 40 Green & Refreshing Website Designs from Designers’Couch
• 25 Creative Blog Header Designs from DesignM.ag
• Data Tables In Modern Web Design from Noupe
• Great Examples Of Coming Soon Pages And How To Create Yours from Spyre Studios
• Showcase of Outstanding Fashion Blogs and Hype Online Outlets from Inspired Magazine
• The Beautiful Art of Japanese Web Design from Woork
• 65 Creative And Stylish Footer Designs of 2009 from 1stwebdesigner
• Headers and Footers that Grab You Coming and Going from Web Design Ledger

The year is coming to an end, and it’s time to review what has happened on this blog over the last twelve months. I’ll start the top ten most read posts, and then list my own favorites.

Let’s start with the top ten most read posts published in 2009 as measured by Google Analytics:

1. Introducing Trident – animation library for Java applications has marked the beginning of the long journey to extract the internal animation layer from Substance and make it available as a general purpose library. Published in February, has around 4,300 reads.
2. Project Marble – augmented reality in Java with JMF, Java3D, NYArToolkit and Trident is about mashing together a few libraries and adding a touch of virtual reality to the real world. Marble has not progressed beyond that entry due to the work i’ve been doing on Trident, Substance and Flamingo. Published in July, has around 3,700 reads.
3. Translucent and shaped windows in JDK 7 talks about the published APIs to manipulate top-level windows. This combined with the inclusion of JXLayer (renamed JLayer) is the only client-facing enhancement in Java 7 known so far. Published in May, has around 3,200 reads.
4. First signs of Nimbus designer in JDK 7 has kept the community hopes of finally seeing the much hyped (at JavaOne and other conferences) visual tool for creating Synth-based look-and-feels. For now Nimbus designer has proven even more elusive than JWebPane hinted to be included in NetBeans 6.9. Published in April, has around 3,100 reads.
5. New Dust skin for Swing applications showcased one of the new skins added in Substance 5.3 based on the artwork done by Rico Sta Cruz and Kido Mariano for Ubuntu. Published in March, has around 2,700 reads
6. Trident part 7 – parallel timelines in Swing and SWT is part of a longer series that talks about the Trident animation library. Published in June, has around 2,400 reads.
7. Revolutionizing media playing in Java talks about a new Java-based media player. Unfortunately it doesn’t seem that much work has been done on this project after the beta 0.7 has been published back in July. Published in March, has around 2,100 reads.
8. New Twilight skin for Swing applications showcased another new skin added in Substance 5.3, inspired by the color schemes of the Bespin web code editor spearheaded by Ben (@bgalbs) and Dion (@dalmaer). Published in April, has around 1,900 reads.
9. Animation blueprints for Swing – main application window has kicked off the deeper look into how Trident animation library can be used to add rich animation effects to Swing and SWT applications. Published in May, has around 1,800 reads.
10. Substance goals for 2009 talked about refining and refocusing the goal of Substance look-and-feel, outlining the five goals that drove the development of this library throughout the year. Published in January, has around 1,800 reads.

While these have been the readers’ favorites, a few entries that didn’t enjoy a wider readership are worth highlighting. These are my personal favorites that were published in 2008:

1. Substance goals for 2009 is the only entry from the “most popular” list that is going to appear here. These five goals have driven all the design and implementation decisions that went into the project over the last 12 months.
2. Why i do open source is for those who wonder why i spend my free time in front of the computer and then give away pretty much everything.
3. The devil is in the details zoomed in on the finer visual details of the Woopra desktop client, including information organization, color palette choices, and translucent overlays. You can continue to demand the same level of pixel loving from Substance 6.0 and beyond, as evidenced by the work on combo boxes, spinners and text components.
4. A peek into Substance internals gives a high level overview of the internal implementation details of Substance and is a good starting point for those who want to explore how the library works.
5. Close your Swing / SWT windows in style demonstrates what Trident can do in just a few lines of code.

If you still have not subscribed, click on the icon below to stay tuned in 2010! Happy New Year!